Seismic risk assessment

The goal of a probabilistic seismic risk assessment is to quantify the effect that future earthquakes will have on a system. For individual structures, this evaluation has conventionally been assessed by decoupling the problem into two parts: the evaluation of the seismic hazard at the site of the structure and the estimation of the vulnerability of the structure (i.e., its response to different ground motion intensity levels). Both results are computed independently and used together to estimate the overall risk of the structure. However, this strategy is not practical for spatially distributed infrastructure systems, such as transportation, electric power, and water distribution networks. The response of these types of systems depends on several geographically separated ground motion intensities, and the computation of their joint probability of occurrence is impractical. Thus, it is more convenient to estimate the seismic risk of these types of systems using Monte Carlo simulations, where the system is subjected to a set of earthquake scenarios. Figure 1 shows the general steps of this evaluation for an example road network. The first step is to sample a set of earthquake scenarios with corresponding ground motion intensities at the location of each component of the system. These intensities are then used to sample the damage to the components, which will reduce their functionality. Finally, the network performance is computed considering the functionality reductions. For the example system shown in the figure, the performance is characterized by the increase in travel times of the road network users.

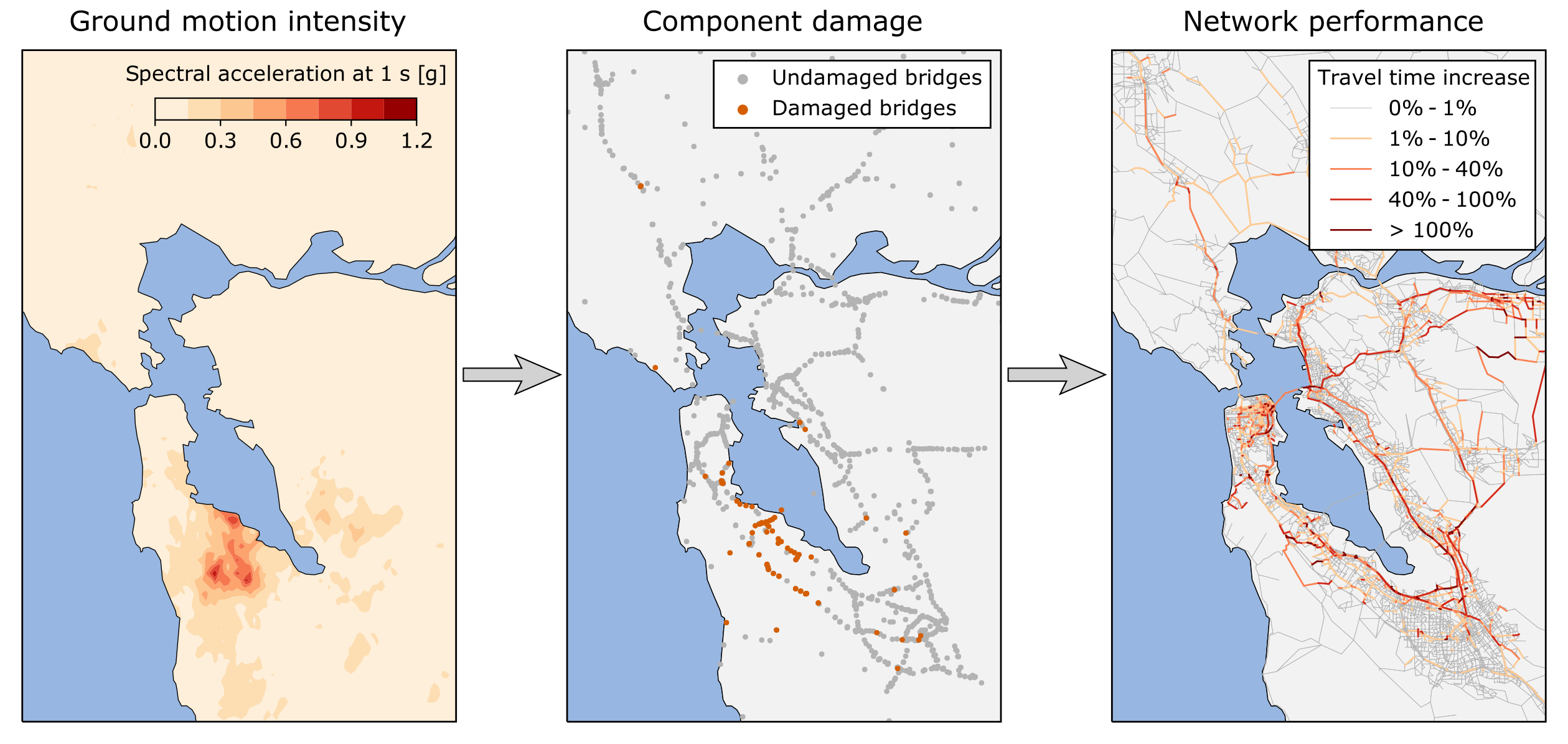
Figure 1: General seismic risk assessment steps to compute the performance of a spatially distributed system for a given earthquake scenario.

I have participated in several studies that applied this method to compute the seismic risk of several systems, including electric power networks in Chile (Espinoza et al., 2020; Ferrario et al., 2022; Oneto et al., 2024) and road networks in the San Francisco Bay Area (Silva-Lopez et al., 2022) and in Chile (Allen et al., 2022). These studies proposed some methodological advances, such as component criticality ranking (Espinoza et al., 2020), uncertainty quantification (Allen et al., 2022), and the use of neural networks to make the evaluation more efficient (Silva-Lopez et al., 2022).

Publications

  1. PDF
    Rosero-Velásquez, H., Monsalve, M., Gómez Zapata, J. C., Ferrario, E., Poulos, A., de la Llera, J. C., and Straub, D. (2024). Risk-informed representative earthquake scenarios for Valparaíso and Viña del Mar, Chile. Natural Hazards and Earth System Sciences , 24, 2667--2687.
  2. HTML
    Oneto, A., Lorca, A., Ferrario, E., Poulos, A., de la Llera, J. C., and Negrete-Pincetic, M. (2024). Data-driven optimization for seismic-resilient power network planning. Computers & Operations Research , 166, 106628.
  3. PDF
    Silva-Lopez, R., Bhattacharjee, G., Poulos, A., and Baker, J. W. (2022). Commuter welfare-based probabilistic seismic risk assessment of regional road networks. Reliability Engineering & System Safety , 227, 108730.
  4. PDF
    Silva-Lopez, R., Baker, J. W., and Poulos, A. (2022). Deep learning-based retrofitting and seismic risk assessment of road networks. Journal of Computing in Civil Engineering , 36(2), 04021038.
  5. HTML
    Ferrario, E., Poulos, A., Castro, S., de la Llera, J. C., and Lorca, A. (2022). Predictive capacity of topological measures in evaluating seismic risk and resilience of electric power networks. Reliability Engineering & System Safety , 217, 108040.
  6. PDF
    Allen, E., Chamorro, A., Poulos, A., Castro, S., de la Llera, J. C., and Echaveguren, T. (2022). Sensitivity analysis and uncertainty quantification of a seismic risk model for road networks. Computer-Aided Civil and Infrastructure Engineering , 37(4), 516-530.
  7. HTML
    Espinoza, S., Poulos, A., Rudnick, H., de la Llera, J. C., Panteli, M., and Mancarella, P. (2020). Risk and resilience assessment with component criticality ranking of electric power systems subject to earthquakes. IEEE Systems Journal , 14(2), 2837-2848.